2003.09.30(火)
▼問題
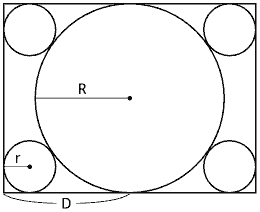
下図のような矩形の横の長さの半分をD、中央の大きな円の半径をRとしたとき、四隅の空間に丁度収まる円の半径rを求めよ。

▼解答
数学は苦手なもんで、素晴らしい解答なのかどーだか知りませんが、とりあえず次のようになると思われます。
大きな円と小さな円の中心を結ぶ直線を引きます。で、その他の線をちょいちょいと下図のように引くと、三角形が現れます。<いきなりテキトーだな(^^;
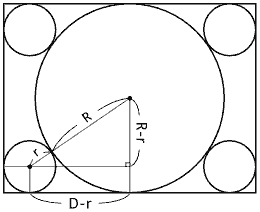
ピタゴラスの三平方の定理(Google検索)により、三角形の各辺の寸法から次式が導かれます。
(R+r)2 = (D-r)2 + (R-r)2
これを展開、移項して整理します。<うわっ、懐かしい響きだ
R2+2Rr+r2 = D2-2Dr+r2 + R2-2Rr+r2
↓
r2 -2(D+2R)r +D2 = 0
rについての二次方程式になりました。これを解けば問題解決です。解の公式を覚えている人は、それにぶちこんでしまいましょう。私はすっかり忘れていたので、何故に公式がそうなるのか、一から勉強ヤり直し(Google検索)。
端折って書けば、ax2+bx+c2 = 0 のとき、x = {−b±(b2−4ac)1/2}/2a となるのですが、テキストで平方を記述するのはわけ分かりませんねぇ。まぁとにかく、それに当てはめると a = 1、b = -2(D+2R)、c = D2 ですから、
r = (D+2R)±{ー2(D+2R)}2ー4D2}1/2
↓
r = (D+2R)±2(R2+DR)1/2
とまぁそんな感じですか。
で、四隅に円を描きたいわけですから、その小円同士が重なるような状態は避けたいです。つまり r ≦ R/2 の条件が付いてきます。上記の式内がすべて加算となると、『2R』の項がある時点で成り立たないですな。てなわけで、答えは次。
r = (D+2R)-2(R2+DR)1/2
これだけを求めるのに、いやー、随分と時間かかっちゃいましたよ(^^; 。中学生んときは「こんなもん将来役に立つのか?」なんて思ってましたけど、役に立つ立たないは別にして、使わなければならないときもあるとゆーわけで。ふぅ。
♪ベンキョーは 出来るうーちに....